Измерительные шкалы

Шкала измерений – это упорядоченная совокупность значений физической величины, которая служит основой для измерения.

Поясним это понятие на примере температурных шкал.

В шкале Цельсия за начало отсчета принята температура таяния льда, а в качестве основного интервала (опорной точки) — температура кипения воды. Одна сотая часть этого интервала является единицей температуры (градус Цельсия). В температурной шкале Фаренгейта за начало отсчета принята температура таяния смеси льда и нашатырного спирта (либо поваренной соли), а в качестве опорной точки взята нормальная температура тела здорового человека. За единицу температуры (градус Фаренгейта) принята одна девяносто шестая часть основного интервала. По этой шкале температура таяния льда равна +32°F, а температура кипения воды +212°F. Таким образом, если по шкале Цельсия разность между температурой кипения воды и таяния льда составляет 100°С, то по Фаренгейту она равна 180°F. На этом примере мы видим роль принятой шкалы как в количественном значении измеряемой величины, так и в аспекте обеспечения единства измерений. В данном случае требуется находить отношение размеров единиц, чтобы можно было сравнить результаты измерений, т.е. t°F/t°C.

В метрологической практике известны несколько разновидностей шкал: шкала наименований, шкала порядка, шкала интервалов, шкала отношений и др.

Измерительные шкалы для определения количественных характеристик объектов (явлений) делят на 3 вида:

1. Шкала порядка - упорядоченный ранжированный ряд размеров, в котором каждый последующий больше предыдущего, хотя сами размеры неизвестны Q₁< Q₂< Q₃<…< Q_j.

Расстановка в порядке их возрастания (убывания) с целью получения измерительной информации по шкале порядка называется ранжированием. При однократном сравнении результат измерений имеет вид Q_i£Q_j по шкале. Если есть возможность провести сравнения несколько раз, то результат измерений Q_j+1£Q_i£Q_j, такой результат измерений является случайным, с вероятностью ошибки следует считаться при Q_i³Q_j, Q_i£Q_j и можно пренебречь, если Q_i>>Q_j или Q_i<< Q_j.

Для облегчения измерений некоторые точки на шкале порядка делают фиксированными им присваиваются значения в баллах или условных единицах и они называются опорными (реперными). Особенностью реперных шкал является то, что баллы (условные единицы) нельзя не складывать, не умножать, не делить, не вычитать, т.к. на шкалах порядка не определены никакие математические операции, но установлены логические операции на основе свойств транзитивности. Например, если один размер больше другого, а тот больше третьего, то и первый больше третьего. Шкалы порядка наименее информативны, по ним нельзя определить на сколько или во сколько раз один размер отличается от другого. Такие шкалы распространены там, где к измерениям не предъявляют высоких требований (спорт, искусство, социология, шкала землетрясений, силы ветра, твердости физических тел и т.п.).

2. Шкала интервалов (разностей) имеет условные нулевые значения, а интервалы устанавливаются по согласованию. Такими шкалами являются шкала времени, шкала длины, температурные шкалы. Шкала интервалов более совершенна и разбита на строго определенные интервалы. Например, шкала летоисчисления: год соответствует периоду обращения Земли вокруг Солнца, может быть разбит на сутки (календарная шкала), сутки на часы, минуты, секунды.

Результат измерений имеет следующий вид: Q_i – Q_j=DQ, размеры Q_i и Q_j остаются неизвестными. На шкале определено сложение и вычитание, т.е. можно определить насколько один размер больше другого.

3. Шкала отношений имеет естественное нулевое значение, а единица измерения устанавливается по согласованию. Например, шкала массы (мы говорим веса), начинаясь с нуля, может быть градуирована по разному в зависимости от требуемой точности взвешивания. Шкала отношений служит для представления результатов измерений, полученных посредством экспериментального сравнения неизвестного размера Q_i = Q с размером Q_j=[Q] по правилу Q/[Q] = q. Значение q показывает во сколько раз измеряемый размер Q больше размера [Q], принятого за единицу измерения, или на сколько единиц он больше нуля. На практике из-за влияния множества факторов:

- случайное число.

На шкале отношений определены любые математические операции, что позволяет вносить в показания, нанесённые на шкалу, мультипликативные и аддитивные поправки.

Шкала наименований — это своего рода качественная, а не количественная шкала, она не содержит нуля и единиц изме­рений. Примером может служить атлас цветов (шкала цветов). Процесс измерения заключается в визуальном сравнении окрашенного предмета с образцами цветов (эталонными образца­ми атласа цветов). Поскольку каждый цвет имеет немало вари­антов, такое сравнение под силу опытному эксперту, который обладает не только практическим опытом, но и соответствую­щими особыми характеристиками зрительных возможностей.

1.10. Вероятностно-статистические и числовые (точечные) характеристики измерений

Случайная величина (СВ), которая в результате опыта принимает значения заранее неизвестные, зависит от случайных причин, которые заранее не могут быть учтены. В ходе проведения измерений основное внимание уделяют закономерностям тех случайных явлений, которые обладают относительной устойчивостью. Случайное событие может появиться в результате испытаний, которые могут быть проведены любое число раз при одних и тех же условиях. Такое событие называют массовым и оно может быть охарактеризовано абсолютной частотой m_i (число появления данного события, число появлений одного и того же значения размера), относительной частотой 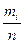, где n – общее число событий. Относительная частота – доля конкретного события в общем числе событий.

Дискретная СВ – называется величина, значения которой отделимы друг от друга и их можно посчитать. Эта величина на любом конечном интервале принимает конечное число значений.

Рис. 5.

Распределение вероятностей.

xi

F(xi)

Рис. 6.

Функция распределения вероятностей.

Результат измерений при дискретном отсчёте характеризуется распределением вероятности (рис. 5) и функцией распределения вероятностей (рис. 6) отдельных значений его Q_i.

За вероятность отдельных конкретных значений принимают его относительную частоту . Функция распределения вероятностей 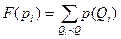сумма p всех значений, пока они не превышают некоторого значения Q. Это функция накопленных частот или кумулятивная.

Непрерывная (аналоговая) величина, отдельные значения которой неотделимы друг от друга и не поддаются счёту, на любом конечном интервале принимает бесконечное число значений.

Для непрерывной аналоговой величины вероятностными характеристиками являются плотность распределения p(Q) и функция распределения F(Q) вероятностей.

Для экспериментальных данных аналогом плотности распределения является 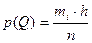, h - относительная частота к цене интервала в нашем случае h = _D Q.

План распределения вероятности представлен в виде гистограммы (рис. 7а) и плотности распределения (рис. 7б).

Рис. 7. а, б – гистограмма и полигон; в – плотность распределения вероятности отсчёта аналогового измерительного прибора.

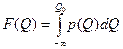
Порядок построения гистограммы:

1. Все экспериментальные данные упорядочиваются и выстраиваются в вариационный ряд.

2. Выбираются крайние значения ряда.

3. Рассчитывается размах измеряемой величины R = Q_max – Q_min.

Задаётся число интервалов разбивки частоты r.

n	r
40…100	7…9
100…500	8…12
500…1000	10…16
1000…10000	12…22

Рассчитываем h = .

4. Определяем границы каждого интервала:

1) Q_min; Q_min + h

2) Q_min + h; Q_min + 2h

3) Q_min + 2h; Q_min + 3h

Для каждого интервала подсчитываются абсолютные частоты, как число экспериментальных данных по своим значениям, попадающим в конкретный интервал.

В каждом интервале рассчитываются относительные частоты 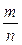. Рассчитывается аналог плотности распределения вероятности 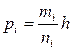. Строят гистограмму с целью графически установить, какому теоретическому закону может соответствовать эмпирическое распределение.

1.11. плотность распределения вероятности p(Q) и функция распределения вероятности F(Q)

Эти две величины служат математическими моделями эмпирических законов распределения, получаемых из экспериментальных данных.

1. Функция распределения вероятности свойств определяет вероятность того, что свойства (отдельный результат измерения) при однократном сравнении не превысят значений аргумента согласно формуле:

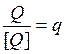; ; x ¹ q.

2. Вероятность не может быть отрицательной, а поэтому функция распределения F(Q) ³ 0. Чем больше Q, тем больше вероятность того, что ни один результат измерения Q не превысит этого значения, т.е. функция неубывающая:

F(Q ₂) > F(Q ₁), Q ₂ > Q ₁.

При изменении Q_i от ∞ до – ∞ F(x) меняется от 0 до 1.

3. Результат отдельного сравнения по формулам больше Q ₁ с вероятностью F(Q ₁) и меньше Q ₂ с вероятностью F(Q ₂).

Вероятность того, что результат сравнения окажется в интервале [ Q ₁; Q ₂] равна разности значений:

P [ Q ₁ ≤ Q ≤ Q ₂] = F(Q ₂) – F(Q ₁).

У аналогового измерительного прибора Q ₁ и Q ₂ можно выбирать сколь угодно близкими друг к другу Q ₁ Q ₂, а F(Q ₂) – F(Q ₁) 0.

4. Плотность распределения вероятности p(Q) связана с функцией распределения F(Q) соотношением:

p(Q) = F′(Q), где

дифференциальная функция распределения вероятности (рис. 8б).

В свою очередь F(Q) может быть получена интегрированием p(Q):

(рис. 8а).

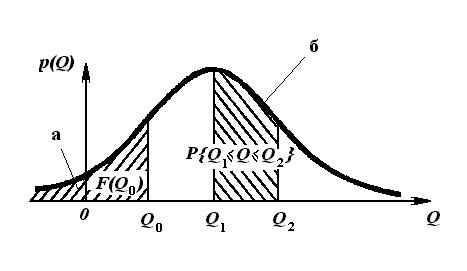
Рис. 8. Геометрическая интерпретация функций F (Q ₀) и p(Q).

5. Так как F(Q) неубывающая функция, то её производная не может быть отрицательной p(Q) ≥ 0.

6. Вероятность того, что Q попадёт в [ Q ₁; Q ₂] равна площади, ограниченной графиком функции p(Q), осью абсцисс и перпендикулярами на границах интервала P [ Q ₁ ≤ Q ≤ Q ₂] = .

7. При расширении интервала до бесконечности рассматриваемое событие достоверно, а площадь ограниченная графиком функции p(Q) и осью абсцисс равна 1.

.

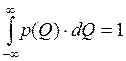Вероятностные статистические характеристики законов распределения наиболее полные, но не всегда удобны и достижимы. Поэтому результат измерений чаще всего представляют в виде числовых характеристик или моментов, представляющих собой некоторые средние значения величин. Моменты называются начальными, если усредняются величины, отсчитываемые относительно начала координат и центральные – при усреднении относительно центра распределения или рассеивания величин.

Правило образования начальных моментов:

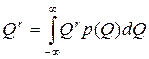, где

r – номер момента.

Важнейшим среди начальных моментов является первый начальный момент:

,

характеризующий математическое ожидание (МО) при бесконечном повторении процедуры сравнения.

Математическое ожидание обозначают M(Q).

Определяют абсциссу центра тяжести распределения масс вероятностей и центр группирования размеров:

, .

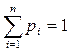Свойства МО:

1. МО неслучайного числа равно самому этому числу:

М(а) = а, а = const.

2. Постоянный множитель можно выносить за знак МО:

М(аX) = а М(X), а = const.

3. МО алгебраической суммы независимых случайных чисел равно алгебраической сумме их МО:

М (х+y–z) = M(x)+M(y) –M(z).

4. МО произведения независимых случайных чисел равно произведению их МО:

М (х·y·z) = M(x) ·M(y) ·M(z).

5. МО отклонения случайного числа от его МО равно нулю:

М [x–М(х)] = 0.

Общее правило образования центральных моментов:

, откуда видно, что первый центральный момент тождественно равен нулю:

.

Второй центральный момент называется дисперсией и обозначается 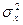или D(x):

.

D – характеризует отклонение размеров около центра распределения. Размерность – квадрат размерности.

В метрологии в качестве меры рассеивания используют среднее квадратичное отклонение (СКО):

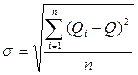- смещенная оценка СКО;

- несмещенная.

Из общего числа данных исключается однозначно = среднему арифметическому.

Свойства дисперсии (D).

1. D неслучайного числа равна нулю:

D(a) = 0, а = const.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат:

D(a·X) = a²·D(X).

3. D алгебраической суммы независимых случайных чисел равна арифметической сумме их дисперсий:

D (х+y+z) = D(x)+D(y)+D(z).

4. D случайного числа равна разности между математическим ожиданием его квадрата и квадратом математического ожидания (рис. 9):

D(x) = M(x²) – M²(x).

X

p(X)

Рис. 9. Графики плотности распределения вероятности отсчёта при различных дисперсиях.

5. Третий центральный момент характеризует асимметрию распределения вероятности:

мерой несимметричности служит

, которая может быть положительной и отрицательной (рис. 10).

X

p(X)

Рис. 10. Симметричное и несимметричные распределения плотности вероятности отсчёта.

Следует отметить, что чем больше дисперсия, тем значительнее рассеивание результатов:

6. Четвёртый центральный момент характеризует степень заостренности кривой распределения вероятности. Мерой заострённости служит эксцесс (рис. 11):

.

X

p(X)

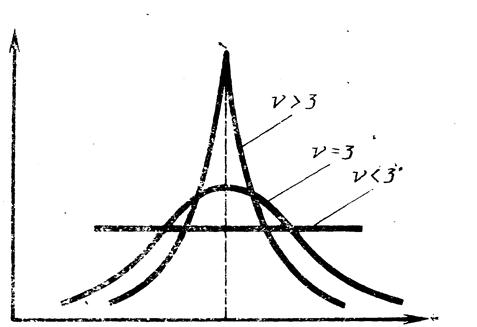
Рис. 11. Дифференциальные функции распределения вероятности отсчёта различной степени заострённости.

Для нормального распределения n = 3.